人工智能-第三周周报
本周任务:https://gitee.com/gaopursuit/ouc-dl/blob/master/week03.md
Deep Residual Learning for Image Recognition:https://arxiv.org/pdf/1512.03385
ResNet⽹络讲解: https://www.bilibili.com/video/BV1T7411T7wa/
Pytorch搭建ResNet⽹络:https://www.bilibili.com/video/BV14E411H7Uw/
Aggregated Residual Transformations for Deep Neural Networks:https://arxiv.org/pdf/1611.05431
ResNeXt⽹络讲解:https://www.bilibili.com/video/BV1Ap4y1p71v/
Pytorch搭建ResNeXt⽹络:https://www.bilibili.com/video/BV1rX4y1N7tE/
概述
这周学习 ResNet 和 ResNeXt
这里先尝试解读两篇论文的内容
Deep Residual Learning for Image Recognition
故事背景
之前我们说过,网络训练的更深还是更宽好?当然是更深更好了
然而传统神经网络极其难训练到很深,而且效果也很差,如论文作者呈现出的这张图中,不论是训练还是测试,56 层的神经网络错误率均明显高于 20 层的神经网络
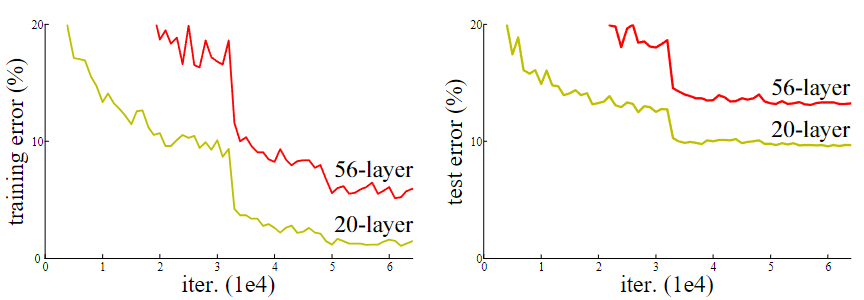
CIFAR-10 20 层和 56 层传统神经网络训练出错率图 (左) 和测试出错率图 (右)
这种现象被称为退化问题(Degradation Problem)
注意
注意区分退化与过拟合(Overfitting)的区别,作者特别提到,退化并不是过拟合导致的
过拟合表现的形式是训练时出错低但是测试的时候出错高,而退化是两种情况都很高
为什么会退化?
文中提到了两点:
梯度爆炸/消失:在之前的文章中我们提出过,越深的网络,梯度是越难控制的,从公式中便能看出。而梯度爆炸/消失现象就会导致严重后果,虽然使用了批量归一化(Batch Normalization)和 ReLU 激活函数等方法缓解了这种现象,然而在网络深度加深的情况下,依然无法避免这种问题
优化困难:经过实验,人们知道,加深网络虽然理论上能得到更好的结果,然而在实际训练中,这样也会导致网络的参数量和运算量巨大,使得优化变得非常困难,比较容易陷入次优解
如何解决这个问题?
作者引入了一个全新的概念,叫做残差学习(Residual Learning)

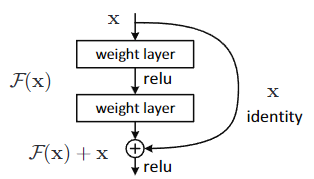
一个残差学习的基本模块
在传统网络中,假如我的 input 是 x ,而需要的 output 是 H(x) ,那么神经网络就需要拟合一个函数,使其能够从 x 变成 H(x),那么在网络很深的情况下,我们发现从 x 学习成 H(x) 是很困难的一件事情,这就像给了你一个鸡蛋,让你想象出鸡的样子
然而作者提到的这个残差学习,是构建一个残差函数,型如:
H(x)=F(x)+xH(x)=F(x)+x
里面的 F(x) 也就是残差,这里的 x 被称为恒等映射(Identity Mapping),通过残差连接(Shortcut Connection)直接传递到输出
通过学习残差而间接得到学习目标,显然是更简单的,也就能达到更好的效果
但是需要注意的是,如果最后得出的 f(x) 与 x 的深度不同,则需要对 x 进行处理,如图中标注的虚线节点处
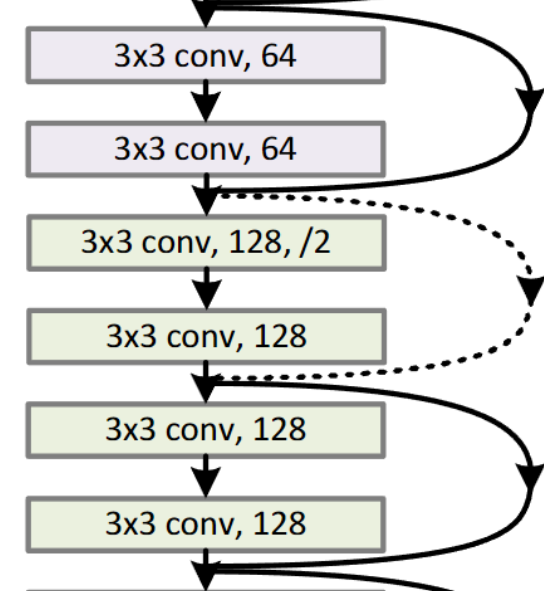
/2 的意思是步长为 2
其中有关这种深度变化的处理,作者提到了两种方法:
Zero-padding shortcut:在深度不足的时候用零矩阵补充不够的深度
Projection shortcut:使用 1x1 的卷积层来调整 x 的通道数
其中关于 Projection shortcut ,作者提到,即使维度一开始就一样,也就是直接做恒等映射,你也同样可以再过一遍 Projection shortcut
以下是不同层数的 ResNet 的结构,一会儿我们写代码的时候会参考这个表
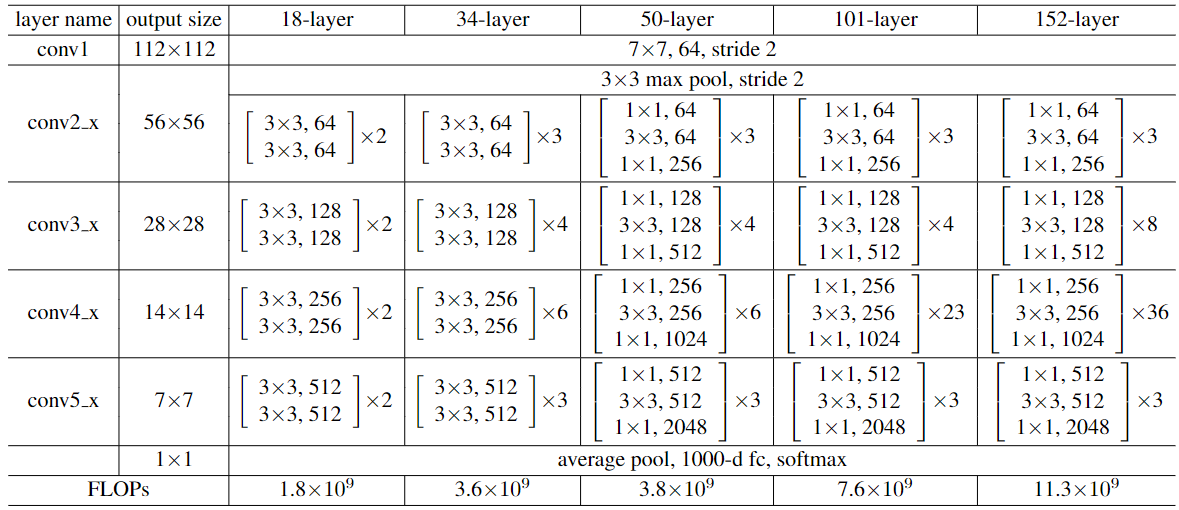
结构图
现在,我们来看看 ResNet 的效果
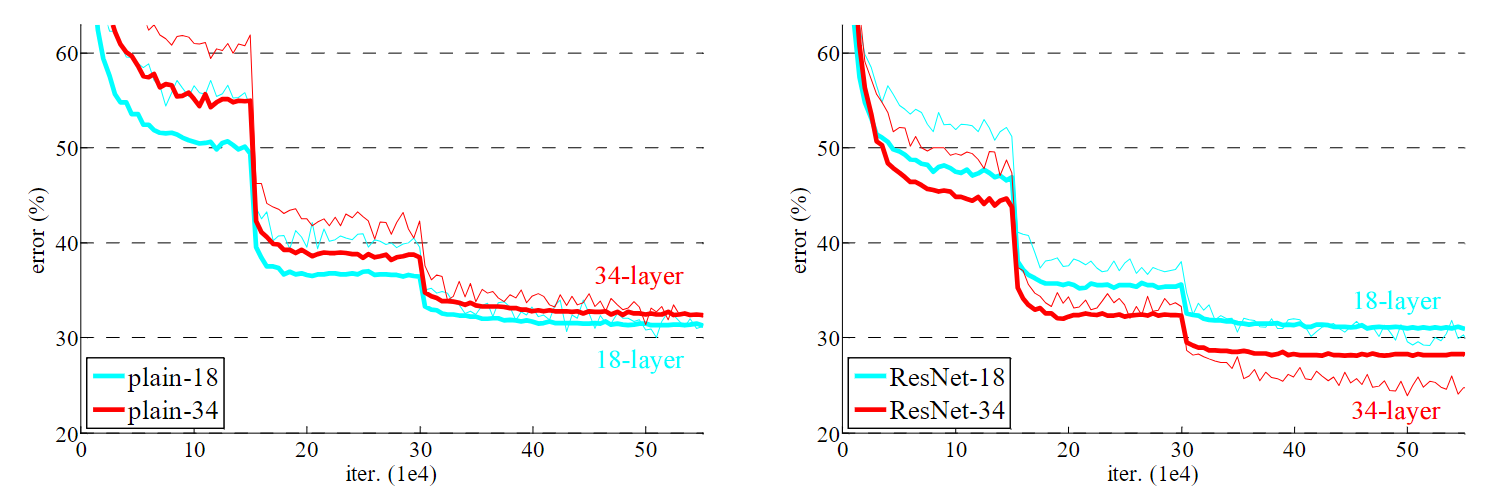
ImageNet 训练,细实线表示训练错误率,粗实线表示中心裁剪部分的验证错误率。18 层和 34 层的普通网络(左)。18 层和 34 层的 ResNet 网络(右)。残差网络与普通网络相比没有额外的参数
可以看出,ResNet 训练更深的网络性能确实更好了,然而,如果需要考虑训练时间等因素,在网络很深的情况下,恐怕就要算到天荒地老了。此时,作者又提出了一个结构,在 ResNet-50/101/152 中使用,叫做瓶颈(Bottleneck)设计,其结构如下图
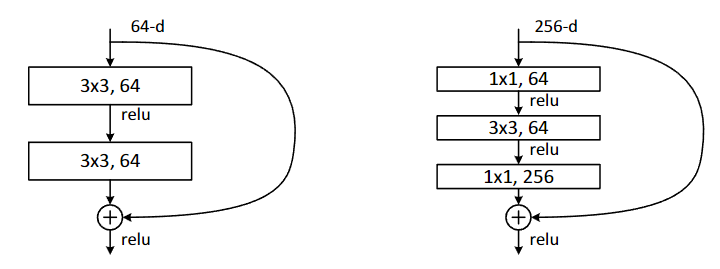
原始ResNet基础结构(左)和瓶颈设计的基础结构(右)
原理是先用 1x1 卷积把深度降下来,处理一次再升回去,从作者给出的结构图中我们可以看到 ResNet-50/101/152 所需的计算量并没有因层数增加而发生爆炸性增长,反而是更加缓和的
基于这个特点,作者之后甚至还构建了一个 1000 层的网络,然而效果并没有想象中表现的那么好,其训练错误率小于 0.1% 而测试时却只有 7.93% ,刚好够看的水平,比 110 层的网络性能还低一些,作者觉得应该是过拟合导致的问题,比较他们没有使用 dropout/maxout 这些的,他们觉得用了以后应该可以更好
迁移学习
在课程中还介绍了迁移学习概念,你可以理解为,在别人已经训练好的模型的基础上,继续训练,其中场景的迁移学习方式有:
1.载入权重后训练所有参数
2.载入权重后训练最后几层的参数
3.载入权重后在原网络基础上再加一层全连接层,仅训练最后一个全连接层
通过迁移学习,可以在更短的时间里获得不错的训练成果,这里我用 ResNet 做了一下迁移学习

迁移学习
可以发现,第一个 epoch 的精度就已经很高了,效果非常不错
代码实现 ResNet
我们先来写一个最基础的模块,也就是我们文章开篇第一张图里展示的结构
class BasicBlock(nn.Module): # 对应 18 层和 34 层 ResNet 的残差结构
expansion = 1
# 对应残差结构中的卷积核个数是否变换,1 为不变
def __init__(self, in_channel, out_channel, stride=1, downsample=None):
# downsample: 下采样当残差块(BasicBlock)主分支的输出特征图与输入特征图的尺寸(高度、宽度)或通道数不一致时,
# 无法直接进行逐元素相加。这时就需要对输入特征图(也就是残差连接)进行下采样操作,使其维度与主分支的输出维度相匹配,以便进行后续的相加操作。
# 相当于 ResNet 论文中标虚线的残差结构
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
kernel_size=3, stride=stride, padding=1, bias=False)
# bias: 偏置,如果 bias 设置为 True,卷积层会在其输出上加上一个可学习的偏置向量。这个偏置项可以增加模型的拟合能力
# 这里设置为 False,因为下面的 BatchNormalization 已经起到了 bias 的作用
self.bn1 = nn.BatchNorm2d(out_channel)
self.relu = nn.ReLU()
self.conv2 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel,
kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channel)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None: # 下采样过程
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out += identity # f(x) + x = H(x)
out = self.relu(out)
return out然后来实现 Bottleneck
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, in_channel, out_channel, stride=1, downsample=None):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
kernel_size=3, stride=1, bias=False) # 压缩 channel
self.bn1 = nn.BatchNorm2d(out_channel)
# --------------------------------------------------------------------
self.conv2 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
kernel_size=3, stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channel)
# --------------------------------------------------------------------
self.conv = nn.Conv2d(in_channels=out_channel, out_channels=out_channel*self.expansion,
kernel_size=1, stride=1, bias=False) # 激励 channel (人话:升维)
self.bn3 = nn.BatchNorm2d(out_channel*self.expansion)
self.relu = nn.ReLU(inplace=True)
# inplace=True 参数表示对输入进行“就地操作”,不分配新的内存空间,直接对原张量进行处理
self.downsample = downsample
def forward(self, x):
indentity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += identity
out = self.relu(out)
return out最后实现 ResNet 类,把这些东西组合起来
class ResNet(nn.Module):
def __init__(self, block, blocks_num, num_classes, include_top=True):
super(ResNet, self).__init__()
self.include_top = include_top
self.in_channel = 64
self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_channel)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, blocks_num[0])
self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2((1, 1)) # 输出大小 (1, 1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
# 凯明初始化(这篇论文的作者之一)
# 功能是对模块 m 的权重 weight 进行原地(inplace)初始化
# fan_in:指当前层的输入神经元(或输入特征)的数量
# fan_out:指当前层的输出神经元(或输出特征)的数量
# nonlinearity: 非线性激活函数,这里选择了 ReLU
def _make_layer(self, block, channel, block_num, stride=1): # block: 基础结构, block_num: 该层叠了几个基础结构
downsample = None
if stride != 1 or self.in_channel != channel * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(channel * block.expansion))
layers = []
layers.append(block(self.in_channel, channel, downsample=downsample, stride=stride))
self.in_channel = channel * block.expansion
for _ in range(1, block_num):
layers.append(block(self.in_channel, channel))
return nn.Sequential(*layers) # *layers: 把列表 layers 中的所有元素解开并将每个元素作为独立参数传递给函数
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
if self.include_top:
x = self.avgpool(x) # 输出: 长 1 宽 1 通道数不变
x = torch.flatten(x, 1) # 变成向量
x = self.fc(x) # 全连接层
return x来试试构建 34 层和 101 层的ResNet吧
def ResNet_34(num_classes=1000, include_top=True):
return ResNet(BasicBlock, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def ResNet_101(num_classes=1000, include_top=True):
return ResNet(Bottleneck, [3, 4, 23, 3], num_classes=num_classes, include_top=include_top)Aggregated Residual Transformations for Deep Neural Networks
背景故事
在 ResNet 的基础上,何凯明又提出了一个新的框架 ResNeXt
摘要中指出,"基数(cardinality)" 也是与神经网络深度和宽度一样,影响性能的一大重要因素,那什么是"基数"呢?可以理解为卷积分支数,如图所示
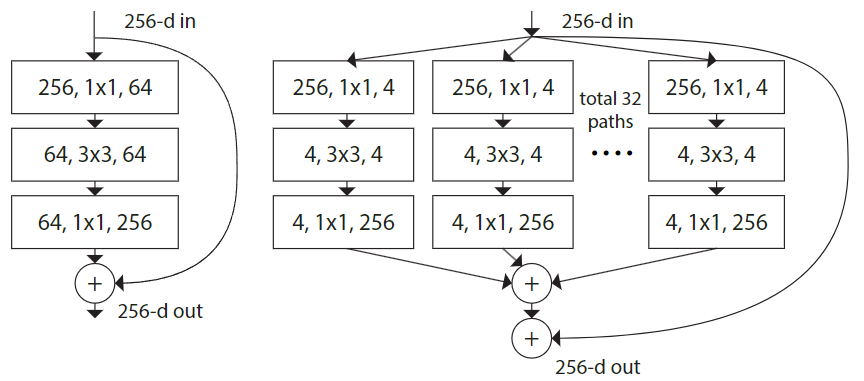
ResNet 的一个基础模块(左)一个"基数"为 32 的 ResNeXt 基础模块(右),他们的复杂度是相同的
其与 ResNet 的结构比较
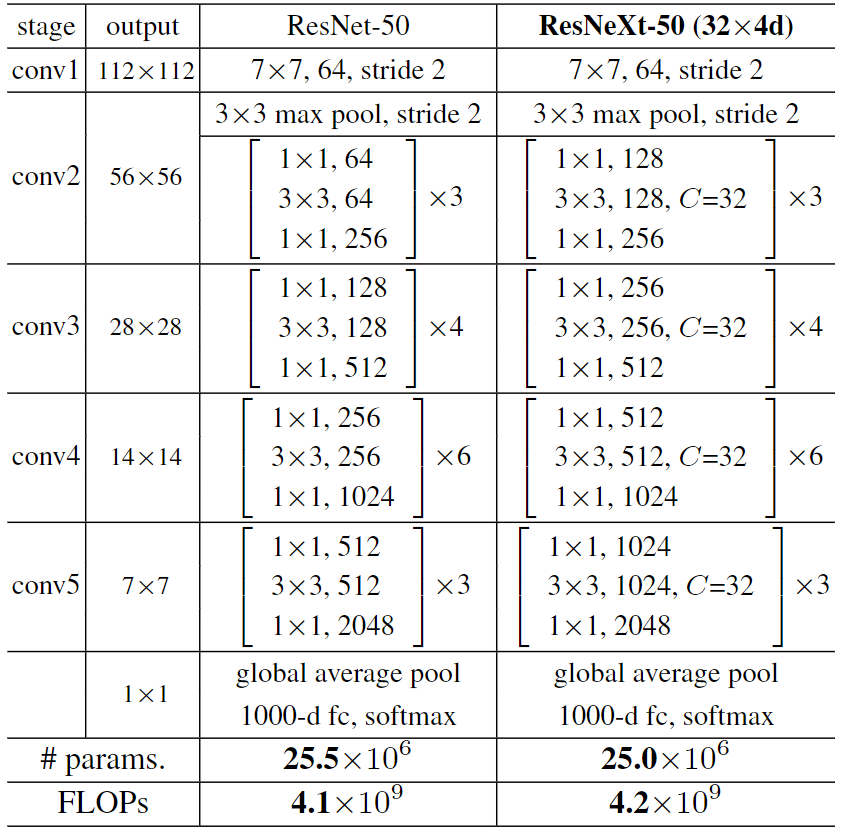
注: 里面的 "C=X" 是指有 X 组卷积分支
而这是他们的性能比较
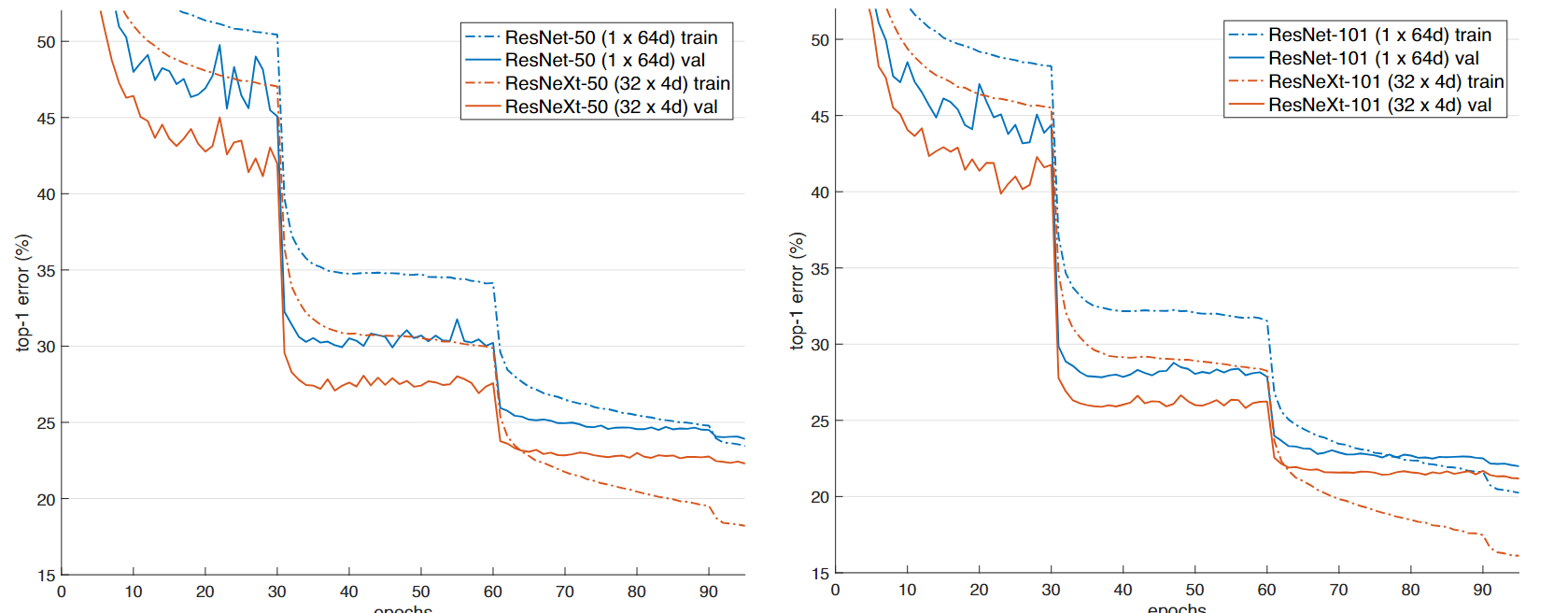
在 ImageNet-1K 数据集上的训练曲线。保持同等复杂度(约41亿 FLOPs,约2500万参数)的 ResNet-50 与 ResNeXt-50 的对比(左);保持同等复杂度(约78亿 FLOPs,约4400万参数)的 ResNet-101 与 ResNeXt-101 的对比(右)
看起来确实不错,那如果用不同的卷积分支组数会怎么样?作者同样给出了回答
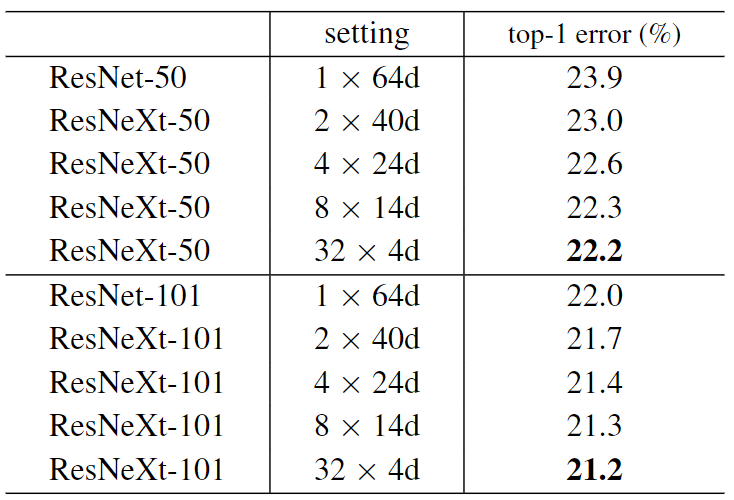
ImageNet-1K 数据集的训练结果
具体其他细节就可以自己去看论文了,这里只放一些比较关键的
代码实现
其实 ResNeXt 和 ResNet 的区别不会很大,也就多了一个分支组的内容,先来实现基础框架
class BasicBlock(nn.Module):
expansion = 1
def __init__(self, in_channel, out_channel, stride=1, downsample=None, **kwargs):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(out_channel)
self.relu = nn.ReLU()
self.conv2 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel,
kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channel)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out += identity
out = self.relu(out)
return outBottleneck
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, in_channel, out_channel, stride=1, downsample=None,
groups=1, width_per_group=64):
super(Bottleneck, self).__init__()
width = int(out_channel * (width_per_group / 64.)) * groups # 不同点
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=width,
kernel_size=1, stride=1, bias=False) # squeeze channels
self.bn1 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv2 = nn.Conv2d(in_channels=width, out_channels=width, groups=groups,
kernel_size=3, stride=stride, bias=False, padding=1)
self.bn2 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv3 = nn.Conv2d(in_channels=width, out_channels=out_channel*self.expansion,
kernel_size=1, stride=1, bias=False) # unsqueeze channels
self.bn3 = nn.BatchNorm2d(out_channel*self.expansion)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += identity
out = self.relu(out)
return outResNeXt 本体
class ResNet(nn.Module):
def __init__(self,
block,
blocks_num,
num_classes=1000,
include_top=True,
groups=1, # 不同点
width_per_group=64): # 不同点
super(ResNet, self).__init__()
self.include_top = include_top
self.in_channel = 64
self.groups = groups # 不同点
self.width_per_group = width_per_group # 不同点
self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_channel)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, blocks_num[0])
self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) # output size = (1, 1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
def _make_layer(self, block, channel, block_num, stride=1):
downsample = None
if stride != 1 or self.in_channel != channel * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(channel * block.expansion))
layers = []
layers.append(block(self.in_channel,
channel,
downsample=downsample,
stride=stride,
groups=self.groups,
width_per_group=self.width_per_group))
self.in_channel = channel * block.expansion
for _ in range(1, block_num):
layers.append(block(self.in_channel,
channel,
groups=self.groups,
width_per_group=self.width_per_group))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
if self.include_top:
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return x来实现一下
def resnet34(num_classes=1000, include_top=True):
return ResNet(BasicBlock, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet50(num_classes=1000, include_top=True):
return ResNet(Bottleneck, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet101(num_classes=1000, include_top=True):
return ResNet(Bottleneck, [3, 4, 23, 3], num_classes=num_classes, include_top=include_top)
def resnext50_32x4d(num_classes=1000, include_top=True):
groups = 32
width_per_group = 4
return ResNet(Bottleneck, [3, 4, 6, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
def resnext101_32x8d(num_classes=1000, include_top=True):
groups = 32
width_per_group = 8
return ResNet(Bottleneck, [3, 4, 23, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)Q: Residual learning 的基本原理?
A: 如文章第一部分
Q: Batch Normailization 的原理,思考 BN、LN、IN 的主要区别
A: 在网络调整权重的时候,因为其他神经元的权重变了,导致其他的神经元也会变,那么,如果网络很深,就会导致这个调整过程异常艰难,这被称为内部协变量偏移(Internal Covariate Shift)
在这种情况下,学习率就不得不变低,就意味着学习缓慢甚至最后直接不收敛了,此时,就可以用 批归一化(Batch Normalization) 了,简称 BN
如果 Batch size 为 m ,那么在向前传递时,网络中每个节点都有 m 个输出,而 BN 则是对这 m 个输出进行归一化后再输出,一般 BN 被插在每个 ReLU 激活层之前
那什么是归一化呢?就是让数据的输出规则规律一些,否则学习数据里面一点分布规律都没有,别说机器了,人类也很难学习
而 BN 的具体任务是将 feature map 中的数据,归一为均值为 0 方差为 1 的数据,对每个通道独立进行运算,而且比较看 Batch Size 的设置,设置太小没什么用,它的具体计算如图
转自 https://blog.csdn.net/weixin_44023658/article/details/105844861 这篇文章写的确实不错
而 LN(Layer Normalization) 是在 (Channel, Height, Width) 这三个维度上计算均值和方差,对每个样本是独立进行的,一般效果不如 BN
IN(Instance Normalization) 只在 (H, W) 这两个空间维度上计算均值和方差,对每个样本和每个通道都是独立进行的,并不依赖 Batch Size
Q: 为什么分组卷积可以提升准确率?既然分组卷积可以提升准确率,同时还能降低计算量,分组数量尽量多不⾏吗?
A: 如上文所说,论文作者在实验的时候发现,并不是分组越多越好的,而是有一个适宜的值,如果分组数量太多,反而会导致准确率下降
通过给卷积分组,就相当于把一个大的、复杂的变换,分成了多个更加简单的变换,显然是更好的,然而,如果分了太多组,就像一个会议如果有太多人说话,最后所有人都别想好,差不多就是这么一个意思了

