
深度学习第一周总结
在第一周的学习中,主要学到了如下内容:
pytorch 中
Tensor相关的基本操作训练螺旋分类模型的基本步骤
激活函数和不同优化器在训练中产生的不同效果
一、学习总结
1. Pytorch 入门
在 4.1 节中,学习了如何使用 Pytorch 中的 tensor 进行基本的张量声明与运算。
(1) 初步认识 Tensor 类型
Tensor包含有存储数据类型dtype和设备信息device。可以通过单值、单维或多维列表、特定 API (如
zeros,ones,rand)进行初始化。也可以利用其他包含数据的
Tensor调用对应的new_*初始化函数以利用原有的存储类型和设备信息。
(2) 初步使用 Tensor 基本运算
可以通过
Tensor.size()访问对应维度的大小,也可以通过Tensor.numel()获取元素总数。可以通过列表式的方括号访问对应维度。
访问到的数据封装在
Tensor类型中。可以以多维切片的方式对每个维度进行截取切分,具体格式为
Tensor[begin1:end1:step1, ..., beginn:endn:stepn]可以使用
@运算符进行矩阵叉乘,且可以自动适配需要转置的矩阵若当前形状不匹配但转置后匹配,则将第二个矩阵进行转置叉乘,再将运算结果转置回来,这体现出了 pytorch 对矩阵横纵轴匹配要求宽松。
矩阵转置过程中,
.t()会自动将单维矩阵补全一个维度,而.transpose(dim1, dim2)不会。需要手动调用
.unsqueeze(1)进行补维。可以使用
Tensor.numpy()将张量转为 numpy 格式并使用 matplotlib 进行绘图。可以使用
torch.randn(n)生成满足均值为 0、方差为 1 的随机数一维张量。结果在宏观上呈现正态分布。
2. 初识螺旋分类训练任务
(1) 数据构造与噪声添加
利用
torch.linspace构造了不同分类下的螺旋形图像公式,并对两维坐标分别传参sin与cos,再通过linspace将图像均匀分布在函数上。在计算坐标过程中,使用了
torch.randn(N)给图像添加了噪声。利用封装好的
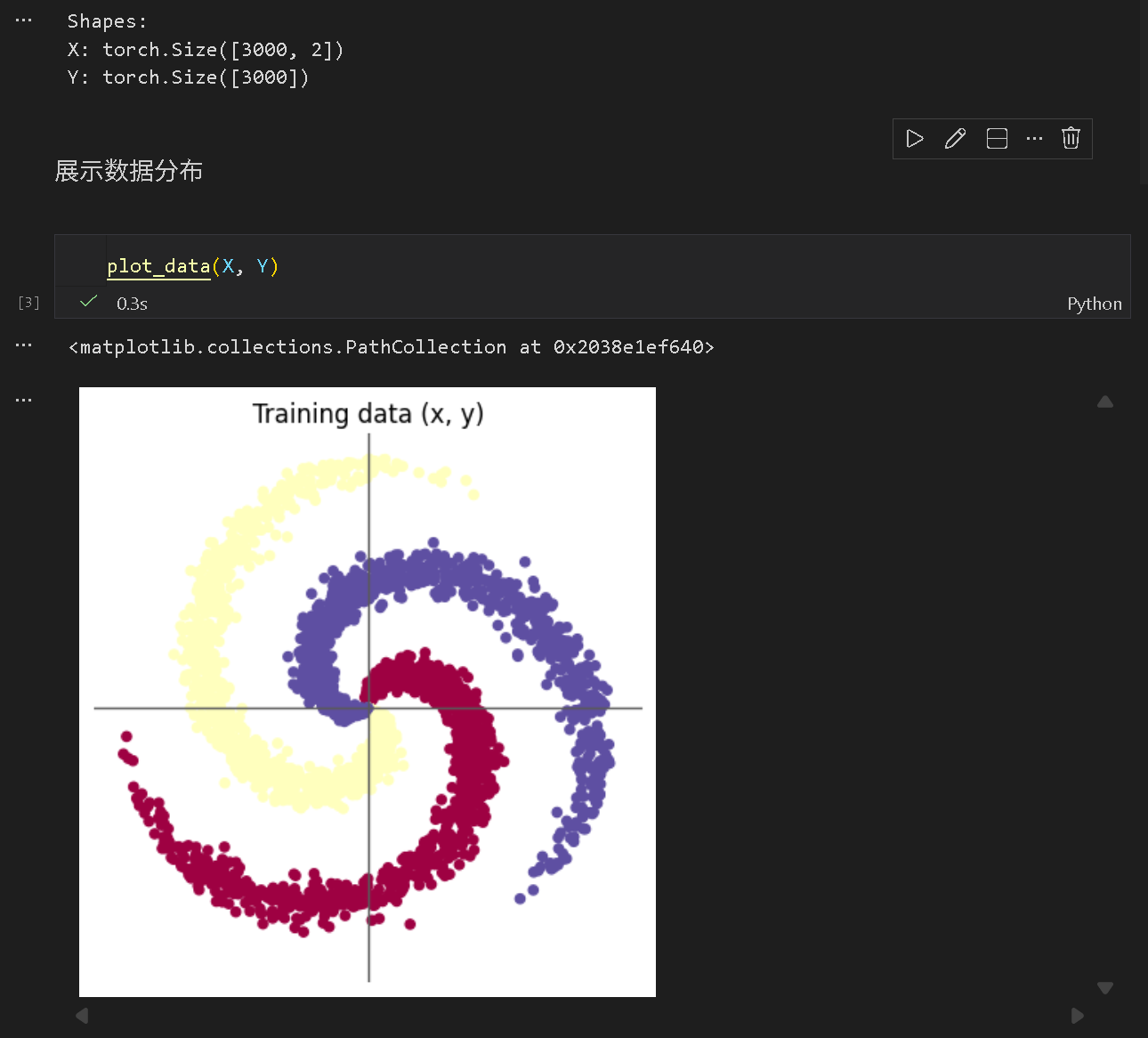
plot_data(X, Y)绘制了螺旋形图像,数据按定义被分类为数个类别。具体实现上同样是调用 matplotlib 对张量在二维平面上进行绘制。
(2) 构建线性分类模型并训练
使用了两层线性层:
D维输入,H维输出
将特征维数通过仿射变换,线性映射为若干隐藏层
H维输入,C维输出
将隐藏层通过仿射变换,线性映射到分类类型上
整体上看,这两个仿射变换层实际上只是组合成了一个更大的仿射变换层,而并没有实现非线性分类。
使用了交叉熵作为损失函数
采用 10^{-3} 的学习率与 10^{-5} 的权重衰减率的 SGD 随机梯度下降优化器进行梯度下降优化。
进行多批次训练,先计算损失值与准确率,再进行反向传播调整,准确率大约收敛在 0.5 左右。
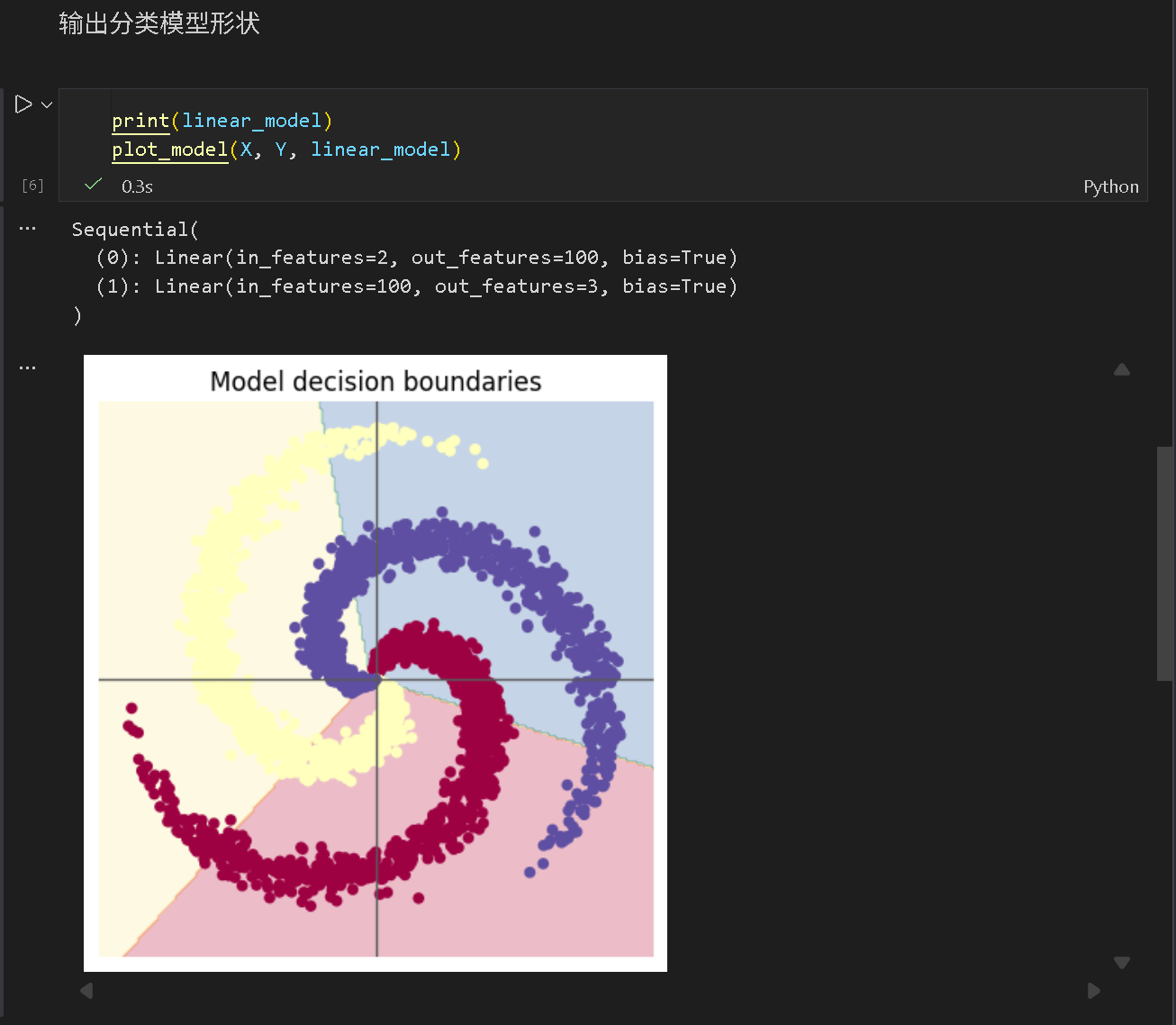
利用封装好的
plot_model对模型分类结果进行输出,观测到线性边界,分类效果不佳。无激活函数,模型缺少非线性层,线性边界缺少在螺旋分类上的灵活性。
(3) 构建两层神经网络并训练
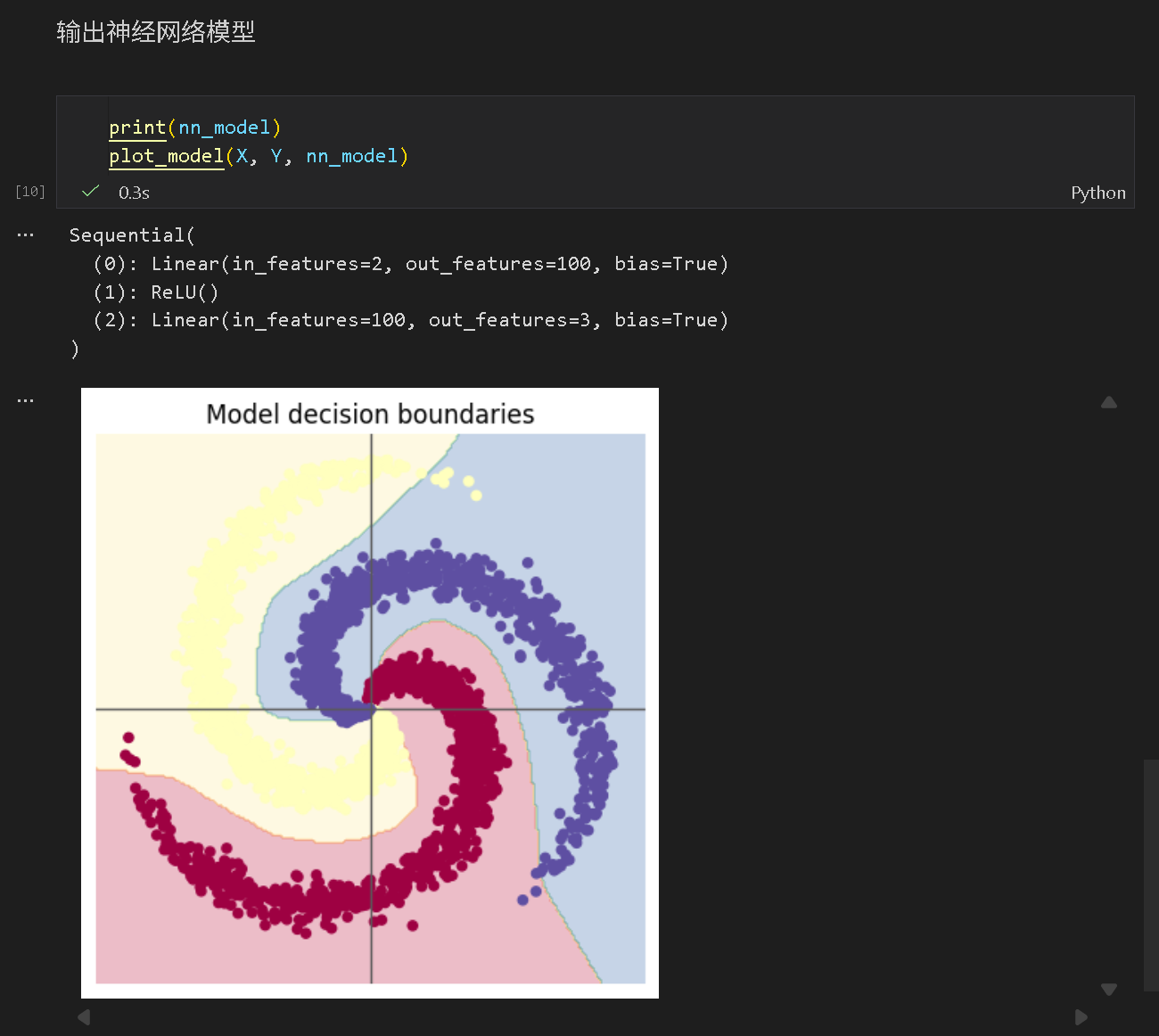
在两层线性层之间添加了 ReLU 激活函数层,实现了非线性变换。
保留损失函数、优化器、学习率等参数不变,进行训练,准确率提升至 0.55 左右,分类效果仍然不佳。
推测:SGD 优化器效果在此任务下效果不佳。
保留其他参数不变,将优化器由 SGD 改为 Adam,准确率暴增至 0.95,表现出了良好的分类效果。
证明了 SGD 在此任务下的表现远低于 Adam。
二、问题总结
1. AlexNet有哪些特点?为什么可以比LeNet取得更好的性能?
答:AlexNet 使用了 5 层卷积,在规模和训练数据量上极大,同时在分类任务中取得了远远领先同时代模型的图像识别方法。它使用 ReLU 而非 tanh 或 sigmoid 作为激活函数,缓解了梯度消失问题,并极大提高了训练速度;它使用 GPU 加速了训练,并以更大的训练数据量提高了训练的精度;在全连接层引入了 dropout 策略有效缓解了过拟合;在训练数据处理上,它采用了随机裁剪、翻转、亮度扰动等多种扩大数据量的技巧。
2. 激活函数有哪些作⽤?
答:激活函数是非线性层,避免了“输出层可以表示为输入层的线性组合”这一特点,可以在训练中形成极为复杂的决策边界,具备拟合复杂数据、处理复杂问题的学习能力。通过改进激活函数,还能提高训练速度、缓解梯度消失等。
3. 梯度消失现象是什么?
答:在反向传播时,靠近输入层的梯度渐趋于 0,导致了学习速度极为缓慢甚至不收敛的问题。反向传播阶段,由于需要利用链式法则进行多层级导数相乘,如果导数小于 1 的居多,则会不断朝更小的方向收敛,直到梯度极小,产生严重的欠拟合现象。可以通过替换不同的激活函数,如 ReLU,以避免梯度的衰减,有效缓解这一现象。
4、神经网络是更宽好还是更深好?
答:在宽度足够学习特征的前提下,适当增加深度比增加宽度带来的训练效果更好。在每层的宽度足够的情况下,多层的神经网络可以“逐层学习不同特征”,从而更能理解复杂任务情景;然而,过深的层数也会带来梯度消失的问题。因此并不是一味添加深度或宽度就能解决问题的,而是要综合深度带来的“模型表达力”和宽度带来的“模型容量”。
5、为什么要使⽤Softmax?
答: Softmax(z_i) = \frac{e^{z_i}}{\Sigma_{j=1}^C e^{z_j}}定义式中可以看出,Softmax 将标签指数化以保留正数、归一化以表示概率。它将标签值转化为了类别的预测概率分布,且具有可微分的特征,可以用于反向传播。
6、SGD 和 Adam 哪个更有效?
答:Adam 更有效。在螺旋分类任务中,SGD 在二层神经网络下准确率仅有 0.55,同情况下改用 Adam 能将准确率提至 0.95。查阅资料可知,SGD 容易振荡或卡在错误方向,而 Adam 利用二阶动量实现了“自适应学习率”,自动调节步长和稳定下降方向,在复杂非凸问题上收敛更快更稳定。
